【第5回】⼈材開発活動に必要なテストの作成⽅法と考え⽅・すすめ⽅
第5回 現代テスト理論
1.古典的テスト理論の限界

この理論は直感的に非常に理解しやすいので、「古典的」という名前は付いていますが、テストの設計や運⽤に現在でも頻繁に利⽤されています。
しかし、⻑年の研究から、いくつかの無視できない限界も指摘されてきました。これら限界にはいろいろありますが、⼤きく分けて以下の3つにまとめられます。
(1) 結果がテストを実施した被験者集団に依存してしまう
(2) 結果がテストそのものに依存してしまう
(3) 古典的信頼性の限界
まずは、これら3つの限界について考えていきましょう。
しかし、⻑年の研究から、いくつかの無視できない限界も指摘されてきました。これら限界にはいろいろありますが、⼤きく分けて以下の3つにまとめられます。
(1) 結果がテストを実施した被験者集団に依存してしまう
(2) 結果がテストそのものに依存してしまう
(3) 古典的信頼性の限界
まずは、これら3つの限界について考えていきましょう。
(1)結果がテストを実施した被験者集団に依存してしまう
例えば、あるテストをA社とB社の両⽅で別々に実施したとします。ただし、テストを構成する項目は両社で共通であるとします。しかしながら、たとえテスト内容が同じであっても、平均値を計算すると両社で異なる値になると考えられます。これは標準偏差や偏差値でも同様です。
A社で求められたこれらの値は、A社のみにしか通⽤しないのです。B社の社員がB社内での⾃分の位置(あるいは⾃分の能⼒や特性)を知るために、A社で求められた値と⽐較しても、何も分かりません。
当たり前のように思うかもしれませんが、テストを考えるときに本質的に重要な点です。
(2)結果がテストそのものに依存してしまう
テストそのものの性質を知りたいのだから、これは⼀⾒すると限界ではないように聞こえます。しかし、テストは1回実施すると受験者に知られてしまい、厳密に⾔えば、2度実施することは基本的にできません。 つまり、テストの結果がテストそのものに依存してしまっていては、たとえ項目の内容を秘匿したとしても、何度も繰り返し実施するのは難しいということです。そのため実施したテストを苦労して標準化したとしても、そのテスト⾃体は使いにくくなってしまっているので、その知⾒を積極的に次に⽣かすことができません。 標準化という⽅法は、既に実施してしまったテストを理解するための⼿段であって、次に実施するテストに対して有効な知⾒(例えば、平均値をテスト実施前に制御するなど)を積極的に与えるような⽅法とは⾔えない側⾯があります。 このためテスト結果がテストそのものに依存してしまう古典的テスト理論では、実社会における現代的なテストの運⽤には耐えられないのです。
(3)古典的信頼性の限界
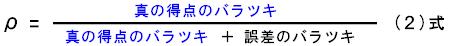
この信頼性係数の⽋点は、この指標がテスト固有のものではなく、「そのテスト」と「それを実施した集団」の組に対して与えられるものであるということです。
では、最⼤でどのくらい⼤きな値を取るでしょうか?
例えば、誤差が0、すなわちテスト得点のバラツキはすべて真の得点によるバラツキのみで説明できると仮定します。その場合、「真の得点のバラツキ = テスト得点のバラツキ」となりますので、(2)式は1となります。
逆にテスト得点が完全に誤差のみで決定されるような場合は、真の得点のバラツキは0となりますので、(2)式は0になります。ここから(2)式は0〜1までの値を取り、1に近いほど信頼性の⾼いテストだと考えることができるでしょう。
そこで、この(2)式をテストの信頼性の指標として採⽤し、信頼性係数ρと名付けます(ρはギリシャ⽂字で「ロー」と読みます)。
例えば、誤差が0、すなわちテスト得点のバラツキはすべて真の得点によるバラツキのみで説明できると仮定します。その場合、「真の得点のバラツキ = テスト得点のバラツキ」となりますので、(2)式は1となります。
逆にテスト得点が完全に誤差のみで決定されるような場合は、真の得点のバラツキは0となりますので、(2)式は0になります。ここから(2)式は0〜1までの値を取り、1に近いほど信頼性の⾼いテストだと考えることができるでしょう。
そこで、この(2)式をテストの信頼性の指標として採⽤し、信頼性係数ρと名付けます(ρはギリシャ⽂字で「ロー」と読みます)。

3.1 同族測定とタウ等化測定
さて、第2回目のコラムでは、テスト得点ではなく5つの項目得点で、(1)式の古典的テストモデルを構成しました。それを以下に再掲します。

上記のような仮定のとき、「項目は互いに同族測定である」といいます。
この同族測定に、さらにもう1つ、以下のような「仮定」を付け加えます。
この同族測定に、さらにもう1つ、以下のような「仮定」を付け加えます。
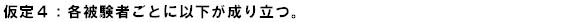
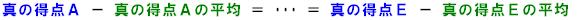
上記の仮定は、「真の得点をその平均値で調整した場合、すべての項目は同じ真の値を測っている」という意味です。このとき、「項目は互いにタウ等化測定である」といいます。
(この仮定は直感的に非常に理解しにくいと思います。しかしここでは、この仮定が「なぜ必要なのか?」と考えるのではなく、「そういうものだ」と納得することをオススメします。)
(この仮定は直感的に非常に理解しにくいと思います。しかしここでは、この仮定が「なぜ必要なのか?」と考えるのではなく、「そういうものだ」と納得することをオススメします。)
3.2 α信頼性係数の算出⽅法
タウ等化測定のもとでは仮定4が追加されました。
仮定4は「真の得点の偏差が項目間ですべて等しい」というものですが、偏差が等しければ当然項目間でバラツキ(分散)も等しくなります。つまり、仮定4は以下と同等です。
仮定4は「真の得点の偏差が項目間ですべて等しい」というものですが、偏差が等しければ当然項目間でバラツキ(分散)も等しくなります。つまり、仮定4は以下と同等です。

このような仮定の下でテスト全体(5項目間)のバラツキを求めると、「25×ある項目1つ分のバラツキ」となります。
ここで「25という数字はどこから出てきたのか?」と思われる⽅がいるかもしれません。あるいは「5項目なのだから『5×ある項目1つ分のバラツキ』でよいのではないか?」と思った⼈もいるでしょう。
しかし、以下のような表で考えるとなぜ25なのかがわかります。
ここで「25という数字はどこから出てきたのか?」と思われる⽅がいるかもしれません。あるいは「5項目なのだから『5×ある項目1つ分のバラツキ』でよいのではないか?」と思った⼈もいるでしょう。
しかし、以下のような表で考えるとなぜ25なのかがわかります。
表1 項目間の(平均調整後の真の得点の)バラツキ
| 項目1 | 項目2 | 項目3 | 項目4 | 項目5 | |
|---|---|---|---|---|---|
| 項目1 | a | f | k | p | u |
| 項目2 | b | g | l | q | v |
| 項目3 | c | h | m | r | w |
| 項目4 | d | i | n | s | x |
| 項目5 | e | j | o | t | y |
つまりここで⾔う「バラツキ」とは、項目単体のバラツキ(表1のa・g・m・s・y)だけではなく、項目1と項目2(表1のb)、項目1と項目3(表1のc)………のように、異なる2項目による共分散※(表1の非対角要素)も含めているのです。そして仮定4ʼとは、「表1のa〜yまでがすべて等しい」ということを意味しています。
⼀般に項目数がN個のときはN2個のバラツキがすべて等しくなります。したがって、信頼性係数を求める (3)式は以下のように再表現されます。
⼀般に項目数がN個のときはN2個のバラツキがすべて等しくなります。したがって、信頼性係数を求める (3)式は以下のように再表現されます。

このようにして、タウ等化測定のもとで計算された信頼性係数のことを「クロンバックのα係数」と呼びます。
α係数は、現在、⾊々なテストを作成するときに、その信頼性の指標として多⽤されますが、このように仮定4という直感的には不⾃然な仮定を前提としています。
そこで「この不⾃然な仮定4を緩和し、同族測定のもとで信頼性係数を構成できないか?」という動きが出てきました。つまり、直感的に理解が容易な仮定1〜仮定3のみで信頼性係数を構成するということです。そこでもう⼀度、古典的テストモデルに⽴ち返ります。
α係数は、現在、⾊々なテストを作成するときに、その信頼性の指標として多⽤されますが、このように仮定4という直感的には不⾃然な仮定を前提としています。
そこで「この不⾃然な仮定4を緩和し、同族測定のもとで信頼性係数を構成できないか?」という動きが出てきました。つまり、直感的に理解が容易な仮定1〜仮定3のみで信頼性係数を構成するということです。そこでもう⼀度、古典的テストモデルに⽴ち返ります。
※ 共分散とは、項目1と項目2のような2組の対応するデータにおいて、偏差(平均との差)の積を算出し、データ数で割ったもの。
例えば、Aさん~Jさんの10⼈が数学と物理のテストを受けたとします。このとき数学と物理の共分散は以下のようになります。
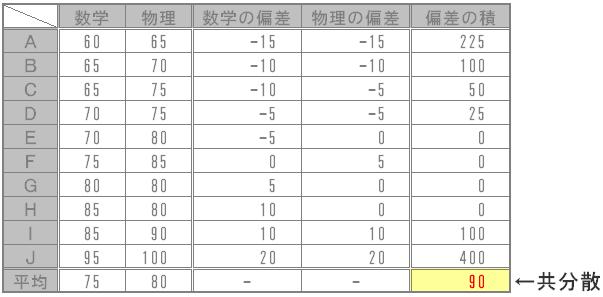
表1のように対角要素にはその項目の分散を、非対角要素に2つの項目の共分散を並べた表のことを、「分散共分散⾏列」と⾔い、データの散らばり具合を表すものとしてよく使われています。
ω信頼性係数の算出⽅法
古典的テストモデルでは、項目得点は真の得点と誤差との和で表現されました。
したがって、バラツキも以下のように分解されます。
したがって、バラツキも以下のように分解されます。
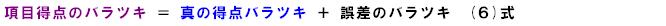
テスト得点は項目得点の総和なので、(6)式をさらに以下のように表現します。

(7)式を少し調整し、
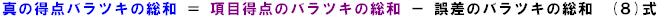
これを(3)式に代⼊して、信頼性係数を再定義します。

このようにして定義された(9)式のことを「マクドナルドのω係数」といいます(ωはギリシャ⽂字でオメガと読みます)。
ω係数は直感的に⾃然(理解が容易)な仮定(同族測定における仮定1〜3)のみで計算されていますので、理論的にもα係数より正確だと考えられます。因⼦分析を使ってテストを設計したときは、α係数だけではなく、ω係数も報告するようにしましょう。
ω係数は直感的に⾃然(理解が容易)な仮定(同族測定における仮定1〜3)のみで計算されていますので、理論的にもα係数より正確だと考えられます。因⼦分析を使ってテストを設計したときは、α係数だけではなく、ω係数も報告するようにしましょう。
今回は、古典的テスト理論の観点から、作成したテストの信頼性と妥当性について解説しました。
そして信頼性と妥当性の2つを同時に確保したテストを作成することがいかに難しいかということを考察しました。
次回は、古典的テスト理論の限界と、それを克服するために考案された最新のテスト理論について解説します。
(担当 : 経営管理研究所 福中 公輔)
